Absolute Value Function
The absolute value function is a rule that involves taking the absolute value
of the input variable. Here are some examples:
| f(x) = |x| |
f(x) = |2x| - 5 |
f(x) = |2x - 3| |
Since we can find the absolute value of any real number, the domain of these
absolute value functions is all real numbers. That is, the interval (-∞,
+∞). The range will depend on the individual
function.
To graph an absolute value function, first calculate several ordered pairs.
Then, plot the ordered pairs on a Cartesian coordinate system. Finally, connect
the points with a line.
Example
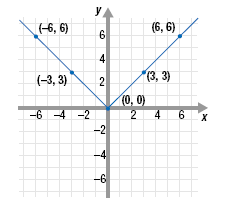
Make a table of five ordered pairs that satisfy the function f(x) = |x|. Then,
use the table to graph the function.
Solution
To make a table, select 5 values for x. We’ll let x = -6, -3, 0, 3, and 6.
Substitute those values of x into the function and simplify.
|
x
|
f(x) = |x| |
(x, y) |
| -6
-3
0
3
6 |
f(-6)
= |-6| = 6
f(-3) = |-3| = 3
f(3) = |3| = 3
f(0) = |0| = 0
f(6) = |6| = 6 |
(-6, 6)
(-3, 3)
(3, 3)
(0, 0)
(6, 6) |
Now, plot the points and connect them.
Notice the
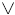 shape of the graph. This is characteristic of the absolute
value function, although sometimes the vee is upside down, like this
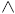 . The point of the vee is called the
vertex.
The domain of f(x) = |x| is all real numbers since we can find the absolute
value of any real number.
To find the range, consider the y-values on the graph. The smallest
y-value is 0. So, the range is y ≥ 0. This is the interval [0,
+∞).
|
