Quotient Rule for Exponents
We can use arithmetic to simplify the quotient of two exponential expressions. For
example,
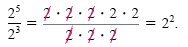
There are five 2’s in the numerator and three 2’s in the denominator. After dividing,
two 2’s remain. The exponent in 22 can be obtained by subtracting the
exponents 3 and 5. This example illustrates the quotient rule for exponents.
Quotient Rule for Exponents
If m and n are any integers and a ≠ 0, then
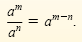
Example 1
Using the quotient rule
Simplify each expression. Write answers with positive exponents only. All variables
represent nonzero real numbers.
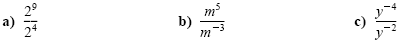
Solution
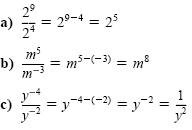
The next example further illustrates the rules of exponents. Remember that the
bases must be identical for the quotient rule or the product rule.
Example 2
Using the product and quotient rules
Use the rules of exponents to simplify each expression. Write answers with positive
exponents only. All variables represent nonzero real numbers.
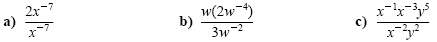
Solution
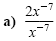 |
= 2x0 |
Quotient rule: -7 - (-7) = 0 |
| |
= 2 |
Definition of zero exponent |
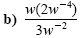 |
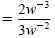 |
Product rule: w1 · w-4 = w-3 |
| |
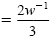 |
Quotient rule: -3 - (-2) = -1 |
| |
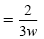 |
Definition of negative exponent |
|