Adding Fractions
How much is 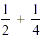 ? (one half + one quarter). ? (one half + one quarter).
Either halves or quarters – which is more convenient?
Should we state how many quarters equal one half or vice versa?
The former, of course: 1 half is 2 quarters . So, the 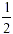 becomes
becomes 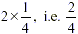 , and the above task becomes , and the above task becomes 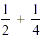 ,
meaning 2 quarters + 1 quarter = 3 quarters, i.e. ,
meaning 2 quarters + 1 quarter = 3 quarters, i.e. 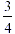 . .
In the above sum, 1 half + 1 quarter, the different types were
associated with the different denominators (dividers), so the
problem was solved by a transformation that led to identical
denominators. Let us now do this for the more general case:
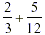 (where we have more than one of each type, namely: 2
thirds and 5 twelfths). (where we have more than one of each type, namely: 2
thirds and 5 twelfths).
Again, we want the same denominators under both, either 3 or
12. Which shall we choose? We must remember that the values of
the fractions must remain unchanged, so, if we change the
denominator, we must also change the numerator (the divided). If
we choose the 3 as the common denominator, we must change the 12
in the second term into a 3, that is, make the denominator 4
times smaller. To keep the value of the fraction unchanged, we
must then also make the 5 on top (the numerator) 4 times smaller,
resulting in 5/4 as the numerator. This is inconvenient because
it creates another fraction above the dividing line.
Instead, we can choose the second denominator, the 12, as the
common one. We leave the 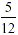 as
it is and change the first denominator, the 3, to 12. This we do
by increasing the 3, by multiplying it by 4. Then, to protect the
value of this fraction, we must also make the numerator (the 2) 4
times bigger, this time giving a manageable whole number, 8. Note
that this resulted from choosing the larger of the two
denominators as the common one. And so, the above as
it is and change the first denominator, the 3, to 12. This we do
by increasing the 3, by multiplying it by 4. Then, to protect the
value of this fraction, we must also make the numerator (the 2) 4
times bigger, this time giving a manageable whole number, 8. Note
that this resulted from choosing the larger of the two
denominators as the common one. And so, the above 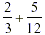 now becomes
now becomes 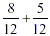 , 8 twelfths + 5 twelfths = 13 twelfths,
i.e. , 8 twelfths + 5 twelfths = 13 twelfths,
i.e. 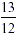 . .
But what about 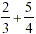 ? ?
To get the first (smaller) denominator (the 3) to be the same
as the second denominator 4, the 3 has to be multiplied by
1.33…, and the same must then be done to the 2 above it,
which results in a messy 2.66…! So we now need a common
denominator which is neither 3 nor 4. In principle, we could
choose anything to put equally at the bottom of both fractions.
The only problem is that we need to adjust the numerators (to
keep the values of the given fractions unchanged) and as we
found, we may only do this by multiplying the numerators by whole
numbers. Form this follows that the denominators, too, can be
changed only by multiplying by whole numbers.
The task becomes: By what whole number do we multiply the 3
(the denominator), and by what (different) whole number do we
multiply the 4 (the other denominator) so that in both cases we
get the same result (namely, the same common, denominator)? The
nice trick for this is to multiply the first denominator (3) by
the second denominator (4) and the second denominator (4) by the
first (3) ! (always, of course, multiplying the numerator by the
same as the denominator).
So this is what was done:
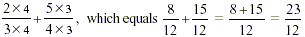
Generalizing:
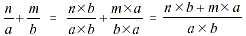
|