Graphing Compound Inequalities
Graphing the Solution Set to a Compound Inequality
The soloution set to a compound inequality such as
x > 2 and x < 5
consists of all numbers that are in the solution sets to both simple
inequalities. So the solution set to this compound inequality is the
intersection of those two solution sets. In symbols,
{x | x > 2 and x < 5} = {x
| x > 2}
Ç {x | x < 5}.
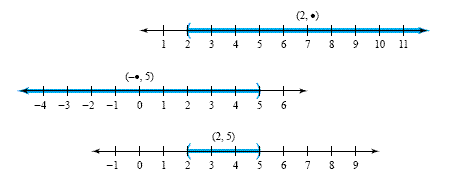
Example 1
Graphing compound inequalities
Graph the solution set to the compound
inequality x > 2 and x < 5.
Solution
We first sketch the graph of x > 2 and then the
graph of x < 5, as shown in the top two number lines in the figure below. The
intersection of these two solution sets is the portion of the number line that
is shaded on both graphs, just the part between 2 and 5, not including endpoints.
The graph of {x | x > 2 and x < 5} is
shown at the bottom of the figure. We write this set in interval notation as (2,
5).
The solution set to a compound inequality such as
x > 4 or x < -1
consists of all numbers that satisfy one or the other or both of the simple
inequalities. So the solution set to the compound inequality is the union of the
solution sets to the simple inequalities. In symbols,
{x | x > 4 or x < -1}
= {x | x
> 4 } È {x
| x < -1}
Example 2
Graphing compound inequalities
Graph the solution set to the compound inequality x > 4 or x < -1.
Solution
To find the union of the solution sets to the simple inequalities, we sketch
their graph as shown at top of the figure that appears below. We graph the union
of these two sets by putting both shaded regions together on the same line as
shown in the bottom graph of the figure. This set is written in interval
notation as
(-∞, -1) È (4,
∞)
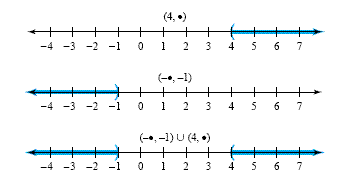
Caution
When graphing the intersection of two simple inequalities, do not draw too
much. For the intersection, graph only numbers that satisfy both inequalities.
Omit numbers that satisfy one but not the other inequality. Graphing a union is
usually easier because we can simply draw both solution sets on the same number
line.
It is not always necessary to graph the solution set to each simple
inequality before graphing the solution set to the compound inequality.We can
save time and work if we learn to think of the two preliminary graphs but draw
only the final one.
Example 3
Overlapping intervals
Sketch the graph and write the solution set in interval notation to each
compound inequality.
a) x < 3 and x < 5
b) x > 4 or x > 0
Solution
a) To graph x < 3 and x < 5, we shade only the numbers that are both less
than 3 and less than 5. So numbers between 3 and 5 are not shaded in the figure
below. The compound inequality x < 3 and x < 5 is equivalent to the simple
inequality x < 3. The solution set can be written as (-∞,
3).
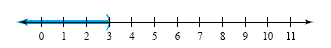
b) To graph x > 4 or x > 0, we shade both regions on the same number line as
shown on the figure below. the compound inequality x > 4 or x > 0 is equivalent
to the simple inequality x > 0. The solution set is (0,
∞)
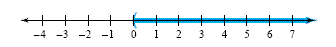
|