Lines and Equations
Given the slope ,m, and a point P(x1 , y1) use the modified point-slope formula : y = m(x − x1 ) + y1
y = m(x − x1 ) + y1
⇒ Substitute the values for m and the point P(x1 , y1) then remove parentheses and collect like terms to
find the equation in the y-intercept form:
y = mx +b
The modified point-slope form: y = m(x − x1 ) + y1 becomes the y-intercept form: y = mx +b
where b = [ y1 − mx1 ]
Examples:
Write an equation of the line that contains the indicated point(s) and meets the indicated
condition(s). Write the final answer in y-intercept form: y = mx +b
#1. P(0, 4), m = - 2; ⇒ y = mx + b for the slope (m) and y-intercept (b = y0).
Substituting directly : b = 4 y = (-2) x + (4) ∴ y = - 2x + 4
#2. P(- 2,- 4), m = 3/2; ⇒ y = m(x − x1 ) + y1 m = 3/2 and P(x1 , y1) → x1 = - 2, y1= - 4
⇒ y = 3/2 [x − (- 2)]+ (- 4) or y = 3/2 x + [(3/2)(+2)+ (-4)] or y = 3/2 x + [ 3 − 4]
∴ y = 3/2 x –1 b = - 1
#3. P(-2,-3); m = 0 [horizontal] (y = b) Lines that are horizontal go through y = y1 ∴ y = - 3
#4. Given points: (3, 2), (5, - 3) Find Dy and Dx directly from the table or the points.
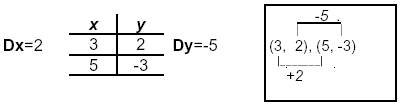
m = - 5/2 x1=3, y1=2 ⇒ y = -5/2 [x - (3)] + (2) or b = 19/2
. ∴ y = - 5/2 x + 19/2
#5. Graph
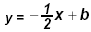 , for b = -3, b = 0, b = 3 or b = {-3, 0, 3} on the same coordinate system.
Plot each y-intercept (0,b) and use
the slope m = -1/2 to graph the lines.
The lines have the same slope so they are parallel.
|
