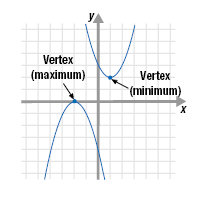
The Vertex of a Parabola
The vertex of a parabola is the point where the curve changes direction.
| • If the parabola opens up, the
vertex is the lowest point on
the graph. This is called the
minimum.
• If the parabola opens down,
the vertex is the highest point
on the graph. This is called
the maximum. |
 |
A vertical line drawn through the vertex is
called the axis of symmetry.
If you fold the graph along the axis of
symmetry one side of the graph will lie on
top of the other.
We can use the following procedure to find the vertex of a parabola.
Procedure — To Find the Vertex of a Parabola y = Ax2 + Bx + C
Step 1 Find the x-coordinate. It is given by the formula
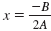 .
.
Step 2 Find the y-coordinate. It is found by substituting the
x-coordinate into y = Ax2 + Bx + C and then simplifying.
Note:
It can be shown that the y-coordinate of
the vertex of a parabola is given by
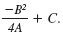
Example 1
Find the vertex of the parabola: y = x2 - 8x + 12
Solution
Here, A = 1, B = -8, and C = 12.
| Step 1 |
Find the x-coordinate.
|
x |
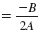 |
| |
Substitute 1 for A and -8 for B. |
x |
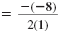 |
| |
Simplify. |
x |
= 4 |
| Step 2 |
Find the y-coordinate.
Substitute 4 for x.
Simplify. |
y y
y
y |
= x2 - 8x + 12 = (4)2
- 8(4) + 12
= 16 - 32 + 12
= -4 |
So, the vertex of y = x2 - 8x + 12 is (4, -4).
Note:
When a parabola has two x-intercepts, the
x-coordinate of the vertex always lies
halfway between the x-intercepts.
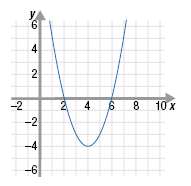
Here the x-intercepts are x = 2 and x = 6. The x-coordinate of the vertex, 4, is
halfway between 2 and 6.
Example 2
Find the vertex of the parabola: f(x) = -2x2 - 12x - 18
Solution
Here, A = -2, B = -12, and C = -18.
| Step 1 |
Find the x-coordinate.
|
x |
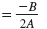 |
| |
Substitute -2 for A and -12 for B.
|
x |
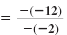 |
| |
Simplify. |
x |
-3 |
| Step 2 |
Find the y-coordinate.
Substitute -3 for x.
Simplify. |
f(x) y
y
y |
= -2x2 - 12x - 18
= -2(-3)2 - 12(-3) - 18
= -2(9) + 36 - 18
= 0 |
So, the vertex of = -2x2 - 12x - 18 is (-3, 0).
Note:
When a parabola has one x-intercept, the
x-intercept is the x-coordinate of the
vertex.
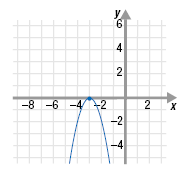
Here the x-intercept is x = -3 and the
x-coordinate of the vertex is x = -3.
|