Solving Systems of Equations by using the Substitution Method
Objective Learn to solve systems of equations
by using the substitution method, and reinforce the geometric
concept of what solving the system means.
Graph the systems after you have found the solutions so that
the geometric idea that the solution corresponds to the
intersection of lines is reinforced.
Solving Systems of Equations Algebraically
You should have solved systems of equations graphically by
graphing the lines corresponding to the two equations and finding
the coordinates of the point of intersection by
“inspection”. Often this method is not good enough
because it is sometimes difficult to get an exact answer.
Instead, there is an algebraic method for solving systems of
equations. Let's begin with an example.
Example 1
Find the solution to the system of linear equations.
3x + y = 3
2x + 5y = 6
Solution
You can graph the equations to get a rough idea of what the
solution set is. The graph of this system of equations is shown
below.
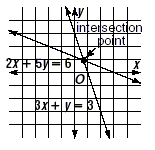
Use the graph to estimate the coordinates of the intersection
point to be about (0.8, 0.9). So, the solution is approximately x
= 0.8, y = 0.9. To find the exact solution, solve the system of
equations algebraically.
Key Idea
Use the Addition and Multiplication Properties of Equality to
solve systems of equations in two variables, just as equations
with one variable are solved.
| 3x + y |
= 3 |
|
| y |
= 3 - 3x |
Subtract 3x from each side. |
This equation is solved for y in terms of x . Since the value
of y must be the same in both equations, substitute 3 - 3x for y
in the second equation.
| 2x + 5y |
= 6 |
|
| 2x + 5(3 - 3x ) |
= 6 |
Substitute 3 - 3x for y. |
| 2x + 15 - 15x |
= 6 |
Distributive Property |
| -13x + 15 |
= 6 |
|
This is an equation involving only one variable, namely x. Now
solve the equation for x.
| -13x + 15 |
= 6 |
|
| -13x |
= -9 |
Subtract 15 from each side. |
| x |
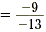 |
Divide each side by -13. |
| x |
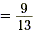 |
|
The exact value for the x-coordinate of the solution is 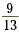 . To find the exact
value for the y-coordinate, substitute . To find the exact
value for the y-coordinate, substitute 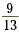 for x in either of the
two equations. for x in either of the
two equations.
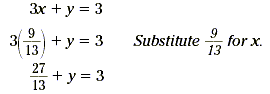
Now use the Subtraction Property of Equality to solve for y.
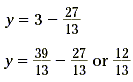
So, the exact solution is given by
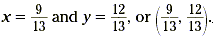
This method always works when the system has exactly one
solution.
|