Multiplying and Dividing Rational Numbers
After studying this lesson, you will be able to:
- Multiply and divide rational numbers
Multiplication and Division Rule (be sure to
learn this rule)
If the two rational numbers have the same sign , their product
or quotient will be positive .
If the two rational numbers have different signs , their
product or quotient will be negative .
For example:
Positive x Positive = Positive
Negative x Negative = Positive
Positive x Negative = Negative
Example 1
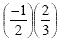
Since we are multiplying a negative times a positive, the
answer will be negative. Remember, you dont need a common
denominator when multiplying fractions. Therefore, the answer
will be 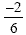 which reduces to which reduces to 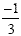 . .
Example 2 ( -3 )(4) Were multiplying a
negative times a positive, therefore the answer will be -12.
Example 3 (-3x) ( -4y) Were multiplying a
negative times a negative, therefore the answer will be 12xy.
(Remember, you dont have to have like terms to multiply.)
Example 4
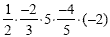
Just as with adding and subtracting, work with two numbers at
a time.
Multiplying the first two fractions will give us 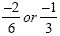 . .
Multiplying 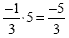
Multiplying 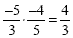 (the fives cancel and a positive times a
positive gives us a positive ) (the fives cancel and a positive times a
positive gives us a positive )
Multiplying 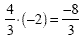
Example 5 ÷ 36 (-4)
Since were dividing numbers with the same signs, the answer
will be positive 9.
Example 6 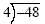
Since were dividing numbers with different signs, the answer
will be -12.
Example 7
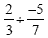
Since were dividing numbers with different signs, the answer
will be negative. We are dividing fractions, so we have to use
the rule for dividing fractions. That rule is multiply by the
reciprocal. First, we change the division sign to multiplication
and we find the reciprocal of the second fraction. Now our
problem looks like this: 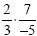 . Multiplying will give us . Multiplying will give us 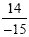 . (note: it does not matter if the
negative sign is in the numerator, the denominator, or is in
front of the fraction.) . (note: it does not matter if the
negative sign is in the numerator, the denominator, or is in
front of the fraction.)
|