Solving Systems of Equations - Two Lines
It is important to note that some equations have decimals or fractions as
coefficients.
Systems do not always have nice integers in the solutions
Example 1:
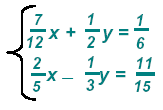
When the equations have fraction coefficients we must multiply each equation by its LCM
to obtain integral coefficients.
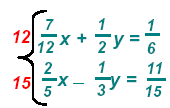 and find
and find
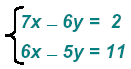
Now we must multiply each equation so that one of the variables has coefficients that are “equal and oppositeâ€.
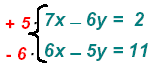 now find
now find
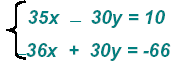
Add the equations
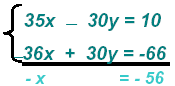 then simplify to get
x = 56 then simplify to get
x = 56
Replace x = 56 in the equation: 7(56) − 6y = 2
→ 392 − 6y = 2 Add opps:
→ - 6y = - 390
multiply recip: → to find y = 65
Check the values in both equations
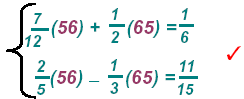 The solution point: { (56, 65) } The solution point: { (56, 65) }
Addition Method:
Add two equations in a system of equations, and obtain another equation in the
system (having the same solution). Also multiply an equation by a real number and obtain another
equation in the system, and combine the two processes.
The object in the Addition Method is to add two of the equations in order to eliminate one of the
variables. The resulting equation can then be solved for either x = h or y = k and which can then
be used as a replacement in one of the given equations to find the value of the other one.
Example 2:
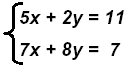
Multiply the first equation by -4

Now add and get
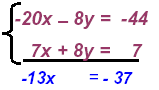
This gives
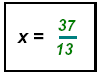
Replace
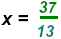 in the first equation:
in the first equation:
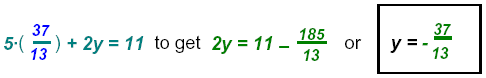
Check the values in both equations
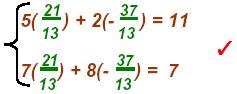
The solution point:
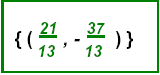
Example 3:
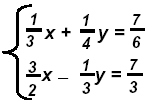
(1) See that the LCM of the 1st equation is 12 and of the 2nd is 6.
(2) Multiply each by the LCM’s
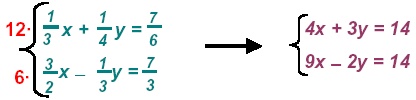
(3) Now solve the simplified system --.
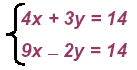 To get equal and opposites multiply the 1st by 2
and the 2nd by +3 then add the results: To get equal and opposites multiply the 1st by 2
and the 2nd by +3 then add the results:
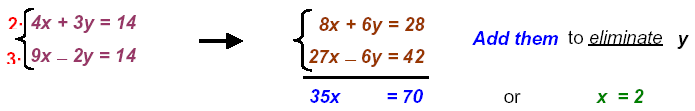
Replace x = 2 in (3): 4(2) + 3y = 14 which yields y = 2
Check: Always check your answers.
Go back to the original equations and substitute both:
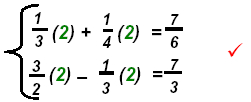
They checked -- now write the solution as S = { (2, 2) }
|