Multiplying and Dividing Fractions
Multiplication of fractions is straightforward, as illustrated
by the following.
Example
Evaluate the following products.
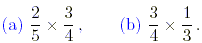
Solution
It is simply a matter of multiplying the numerators and
denominators.
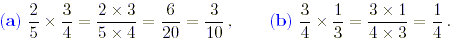
In each case the common factors have been cancelled to leave
the fraction in its lowest form.
Division of fractions is straightforward once we note that
division by a fraction of the form a/b is equivalent to
multiplication by the fraction b/a. This can be seen in the
following example.
Example 5
Write the following as fractions in the usual way.
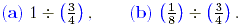
Solution
(a) First note that
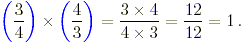
Divide both sides of this equation by (3/4)
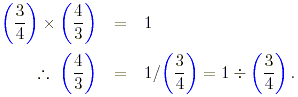
(b) The previous result may be used.
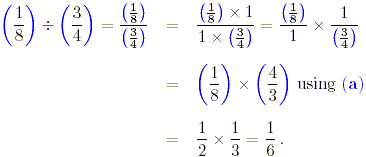
where a common factor 4 has been cancelled.
Exercise 3.
Evaluate each of the following in their lowest terms.
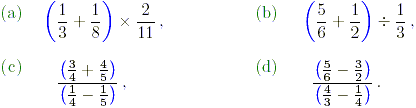
(a) Using exercise 2 part (a) we have
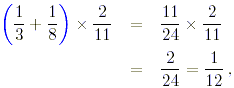
where the common factors of 11 and then 2 have been cancelled.
(b) Using the result of exercise 2 part (b)
we have
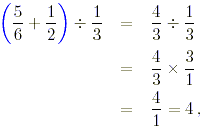
after recalling that division by 1/3 is the same as
multiplication by 3/1=3, and cancelling the common factor 3.
(c) From exercise 2 part (c), the numerator
is 31/20. The denominator is evaluated below.
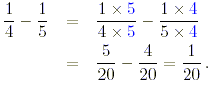
Thus
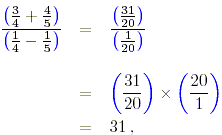
after cancellation of the common factor 20.
(d) In this case, from exercise 2 part (c),
the denominator is 13/12. Evaluating the numerator,
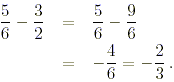
after cancelling the common factor 2. Thus
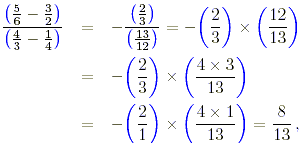
after cancellation of the common factor 3.
|