Solving Quadratic Equations
Converting Standard Form to Vertex Form
Completing the Square
You can covert any quadratic formula from standard form:
y = a · x 2 + b
· x + c,
to vertex form:
y = a · (x - h) 2 + k,
through an algebraic process called completing the square. The next example
demonstrates the steps that are involved in this process.
Example
Convert the quadratic function:
y = 4 · x 2 + 6
· x + 7,
from standard to vertex form and locate the x- and y-coordinates of the vertex.
Solution
Once the formula for the quadratic function has been converted to vertex form:
y = a · (x - h) 2 + k,
we can find the vertex by checking the vertex form to find the values of h (which will be
the x-coordinate of the vertex) and k (which will be the y-coordinate of the vertex).
Conversion of the formula from standard to vertex form is a four-step process called
completing the square.
1. Factor out the coefficient of x2 from all terms.
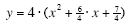
2. Add and subtract just the right amount1 to create a perfect square
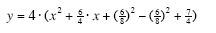
1 To find just the right amount, you take the number that is left multiplying the x after Step 1 has been
completed. Whatever this number is, divide the number by 2 and then take the square of what you are left
with. This is just the right amount to create a perfect square.
3. Factor the perfect square and combine the constants
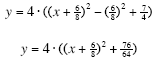
4. Distribute the factor that is out in front of the equation
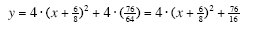
The vertex form of the quadratic function is:
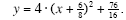
This is not quite the same as the “classic†format of the vertex form:
y = a · (x - h) 2 + k,
because the number inside the parentheses is added to x, rather than subtracted from x.
To fix this we can use the fact that the negative of a negative is a positive, so that
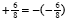 . Using this to re-write the vertex form in the “classic†format gives:
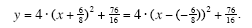
With the vertex form in the “classic†format you can go ahead and determine the x- and
y-coordinates of the vertex. The x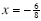-coordinate is
 and the y-coordinate is
|
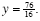
