Adding and Subtracting Fractions

Addition (when the denominators are the same)

Add the numerators. Keep the same denominator.

Adition: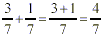

Subtraction (when the denominators are the same)

Subtract the numerators. Keep the same denominator.

Subtraction: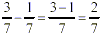

Common Denominators

Since we can change the form of a fraction by multiplying the top and bottom by the same thing, we can force any two fractions to have the same denominator. The trick is to give both denominators all the same factors.

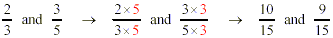
Note that if the denominators we want to match are 3 and 5, we can multiply 3 by 5 and 5 by 3 to convert both fractions to 15ths. (We actually didn’t change the fractions in the process, because we multiplied both top and bottom of each fraction by the same number in each case. That’s what keeps it all “legal.”)

Least Common Denominators

If two denominators have some factors in common, simply multiplying the denominators together will give you needlessly big numbers that have to be reduced later. Instead, spread out and compare the factors of both denominators and multiply each denominator by the factors it lacks.

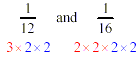
Notice that both denominators contain 2 × 2 (marked in blue), but one has an extra 3 and the other has two more extra 2’s. If the first fraction is multiplied (top and bottom) by 4 ( = 2 × 2 ) and the second fraction is multiplied (top and bottom) by 3, all the factors in both denominators will match.

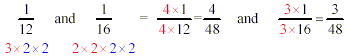
The little bit of extra work breaking the denominators into factors at this stage is easier than multiplying 12 by 16 and 16 by 12 (= 192), because you would then have to turn right around and reduce the resulting fractions which would by then involve much larger numbers.

Addition or Subtraction when the denominators are NOT the same

Convert the fractions to equivalent fractions having the same denominator, then add or subtract the numerators as before.
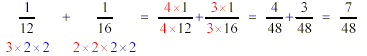