Simple Trinomials as Products of Binomials
Examples with solutions
Example 1:
Factor x 2 – 2x – 35 as completely as
possible.
solution:
The terms of this expression contain no common monomial
factors. However, since this expression has the form of a
trinomial in x, with the coefficient of x 2 being 1,
factoring into the product of two binomials, (x + a)(x + b) may
be possible. We would need to find values for a and b satisfying
a + b = -2
and
ab = -35
As in the previous example, we begin by making a table of all
pairs of whole numbers which multiply to give, in this case, -35.
The easiest way to make sure our list is complete is to make sure
that the value of ‘a’ covers all positive and negative
whole numbers which divide evenly into -35. The value of
‘b’ in each case is obvious, because we need to have ab
= -35.
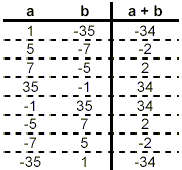
It appears that there are eight candidate pairs of whole
numbers that multiply to give -35. (However, if you examine the
table carefully, you’ll see that only four of these pairs of
values are unique. The last four rows essentially duplicate the
first four rows, amounting to swapping the order of the two
possible factors in the eventual product. So, we’ve done
twice as much work here as was really necessary.)
To achieve the proposed factorization, one of these pairs of
numbers must sum to -2. From this table, this is seen to occur
when a = 5 and b = -7. Thus, it appears that
x 2 – 2x – 35 = (x + 5)(x – 7)
is the required answer.
Checking,
(x + 5)(x – 7) = x(x – 7) + 5(x – 7)
= x 2 -7x + 5x – 35
= x 2 - 2x – 35
confirming our answer.
Example 2:
Factor as completely as possible: x 2 + 8x + 10.
solution:
There are no common monomial factors here, but the expression
has the form of a trinomial of the type considered in the
previous two examples. Thus, a possible factorization has the
form of a product of two simple binomials, (x + a)(x + b), if we
can find two numbers, a and b, satisfying
a + b = 8
and
ab = 10
Setting up the usual table of pairs of whole numbers with a
product of +10, we get
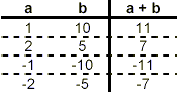
(Here, we listed values of ‘a’ which divide evenly
into +10, only for |a| < |b|, realizing from the previous
example that to also include rows in the table for a = ± 5 and a
= ± 10 will just duplicate the information in these first four
rows.)
To get this factorization to work, we need to find a pair of
these whole numbers which sum to 8. However, the table contains
all possibilities, and none of the rows give a sum of 8. So, we
must conclude that the given trinomial cannot be factored.
In the special situation that a = b, we get the form
(x + a)(x + a) = (x + a) 2 = x 2 + 2ax +
a 2
Thus, a trinomial in which the coefficient of x 2
is 1 is the square of a binomial if
(i) the constant term is a perfect square (of a whole number)
and
(ii) the coefficient of the x term is double the square root
of the constant term.
You don’t really need to memorize this formula as a
special case, because the more general method described above
will also work in this case. You’ll just find that the two
whole numbers, a and b, that you get from the analysis will be
equal.
|