Dividing Fractions
The objective of this lesson is that you learn how to divide fractions correctly.
Numerator and Denominator
The number or algebraic expression that appears on the top line of a fraction is called the
numerator of the fraction.
The number of algebraic expression that appears on the bottom line of a fraction is called
the denominator of the fraction.

Dividing Fractions
Expressed in symbols, the rule for dividing one fraction by another is as follows:
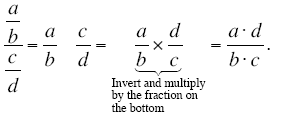
The rule for dividing one fraction by another is usually called inverting and
multiplying. To divide one fraction by another, you “flip†(or “invertâ€) the fraction on
the bottom and then multiply.
Example
Work out each of the following divisions of fractions.

Solution
(a)
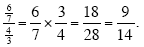
(b)
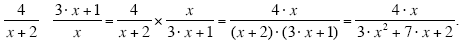
When you get to the multiplication step of these calculations, you have to remember to
multiply entire quantities by entire quantities (which will usually involve FOILing). For
example, after the fraction has been inverted, the multiplication involves multiplying (x +
2) by (3·x +1). Multiplying these two quantities together will require you to FOIL the
two brackets.
(c)
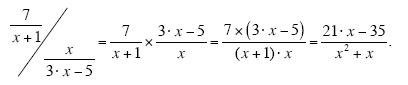
Again, note the necessity for FOILing once the inversion has been carried out and the
multiplication is begun.
Dividing Numbers by Fractions
It is sometimes confusing to work out the result when a number is divided by a fraction.
The key thing to bear in mind here is that a number is the same as a fraction – you just
use a denominator of “1.â€
Example
Simplify:
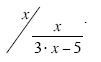
Solution
You can covert this to a fraction division problem by writing the fraction
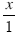 instead of the
“number†x. instead of the
“number†x.
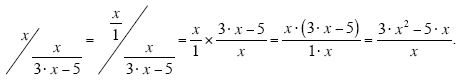
This is certainly simpler than it was, but is not the simplest format that is possible. Each
of the terms in the numerator has a common factor of x, which can be factored out and
canceled with the x in the numerator (provided x " 0).
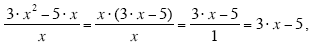 provided x
≠ 0. provided x
≠ 0.
Dividing Fractions by Numbers
You can also deal with potentially confusing problems in which fractions are divided by
numbers by converting the numbers to fractions. This will convert the confusing problem
into a fraction division problem.
Example
Simplify:
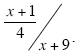
Solution
Again, the key is to write the “number†as the fraction
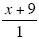 instead of just the “numberâ€
x + 9. This converts the problem into a fraction division problem that you can solve by
“inverting and multiplying.†instead of just the “numberâ€
x + 9. This converts the problem into a fraction division problem that you can solve by
“inverting and multiplying.â€
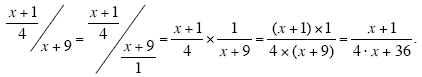
|