Multiplication Property of Exponents

Exponents have several properties. We will use these properties to simplify expressions. In the properties that follow, each variable represents a real number.

Multiplication Property

Property — Multiplication Property of Exponents

English To multiply two exponential expressions with the same base, add their exponents. The base stays the same.

Algebra x^m · xⁿ = x^{m + n} (Here, m and n are positive integers.)

Example 5⁴ · 5² = 5^{4 + 2} = 5⁶

Example 1

a. Use the Multiplication Property of Exponents to simplify 2³ · 2⁴.

b. Use the definition of exponential notation to justify your answer.

Solution

a. The operation is multiplication and the bases are the same. Therefore, add the exponents and use 2 as the base.

2³ · 2⁴ = 2^{3 + 4} = 2⁷

b. Rewrite the product to show the factors. Then simplify.

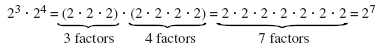
Note:

Remember to add the exponents, but leave the bases alone.

That is, 2³ · 2⁴ = 2^{3 + 4} = 2⁷ , not 4⁷.

Note the difference between 2³ · 2⁴ and 2³ + 2⁴.

2³ · 2⁴ = 2^{3 + 4} = 2⁷ = 128

2³ + 2⁴ = 8 + 16 = 24

Caution — Negative Bases

A negative sign is part of the base only when the negative sign is inside the parentheses that enclose the base.

For example, consider the following cases:

In (-3)², the base is -3.

(-3)² = (-3) · (-3) = +9

In -3², the base is 3.

You can think of -3² as the “opposite” of 3².

-3² = -(3 · 3) = -9

Example 2

If possible, use the Multiplication Property of Exponents to simplify each expression:

a. ( 2)² · ( 2)⁴

b. 2² · 2⁴

c. 2² · ( 2)⁴

c. In -2² · (-2)⁴, the base of the first factor, -2², is 2.

The base of the second factor, (-2)⁴, is -2.

The bases are not the same, so we cannot use the Multiplication Property of Exponents.

However, we can still evaluate the expression. -2² · (-2⁾⁴ = -4 · 16 = -64