Solving Linear Equations Containing Fractions
To solve a linear equation that contains fractions, it is often helpful to first
clear the fractions. Then the equation can be solved using the steps for
solving a linear equation.
One way to clear the fractions is to multiply both sides of the equation by
the least common denominator (LCD) of the fractions. The LCD is the
smallest positive number that is evenly divisible by all of the denominators
in the equation.
Here is a procedure for finding the LCD of a set of fractions.
Procedure
To Find the Least Common Denominator (LCD)
Step 1 Factor each denominator into its prime factors.
Step 2 List each factor the greatest number of times that it appears
in any one of the denominators.
Step 3 Multiply the prime factors in the list.
Example 1
Find the LCD of
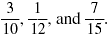
Solution
| Solution
Step 1 Factor each denominator
into its prime factors. |
10 = 2
· 5
12 = 2 · 2 · 3
15 = 3 · 5 |
| Step 2 List each factor the greatest
number of times that it appears
in any one of the denominators.
Step 3 Multiply the prime factors in the list.
|
2, 2, 3, 5 2 · 2 · 3
· 5 = 60 |
The LCD of
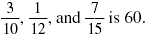
That is, 60 is the smallest number that is evenly divisible
by 10, 12, and 15.
Now, let’s solve an equation that contains fractions.
Example 2
Solve:
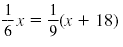
Solution
First, find the LCD of the fractions. The LCD is the smallest number that
is evenly divisible by 6 and 9. The LCD is 18.Next, clear the fractions:
| • Multiply each side by the LCD, 18.
|
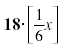 |
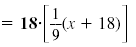 |
| • Simplify.
Then, solve the equation for x:
• Remove the parentheses.
• Subtract 2x from both sides.
We leave the check to you.
The solution is x = 36. |
3x
3x
x |
= 2(x + 18)
= 2x + 36
= 36 |
|