|
Subtracting Fractions
Expressed in symbols, the rule for subtracting one fraction
from another is as follows:
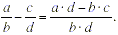
Let’s break this down to see everything that is expressed
in this rule. The numerator of the sum is a · d - b · c . This
is almost exactly the same as the pattern of cross-multiplying.
The only difference is that because the fractions are subtracted,
a minus sign now joins the a · d to the b · c .
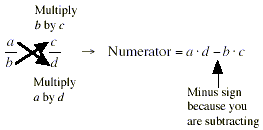
To get the denominator of the sum, you just multiply the two
denominators ( b and d ) together.
Example
Work out each of the following differences of fractions.
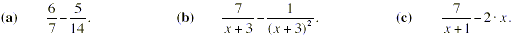
Solution
(a) You can work out this difference in the
two fractions using the given rule for finding the difference of
two fractions:
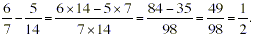
This fraction subtraction can also be accomplished in a
slightly more efficient way by noticing that the two denominators
that are involved (i.e. “7” and “14”) are
related because “14” is a multiple of “7”
(i.e. 7 × 2 = 14).
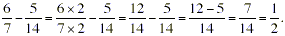
(b) You can work out this difference of two
fractions using the standard rule for subtracting two fractions:
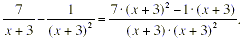
You can then simplify further by FOILing and collecting like
terms. Note that when - 1 · ( x + 3) is expanded the negative
sign multiplies both the x (to create - x ) and the
“+3” (to create the - 3).
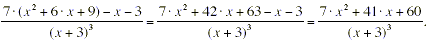
You could also FOIL out the ( x + 3)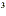 that appears in the denominator, but it is a matter of opinion as
to whether or not that actually makes the fraction any simpler.
There is a more efficient way of subtracting these two fractions.
This more efficient way is possible because the two denominators
(i.e. ( x + 3) and ( x + 3)
that appears in the denominator, but it is a matter of opinion as
to whether or not that actually makes the fraction any simpler.
There is a more efficient way of subtracting these two fractions.
This more efficient way is possible because the two denominators
(i.e. ( x + 3) and ( x + 3)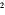 ) are related because ( x + 3)
) are related because ( x + 3)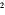 is a multiple of ( x + 3). The more efficient thing to do is to
multiply both the numerator and denominator of
is a multiple of ( x + 3). The more efficient thing to do is to
multiply both the numerator and denominator of 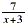 by ( x + 3). Doing this: by ( x + 3). Doing this:
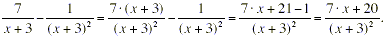
Although the two answers look different, they are actually the
same because:
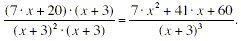
(c) Although the subtraction:
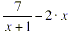
does not initially appear to be a subtraction that can be
carried out using the usual rule for fraction subtraction, it is
possible if you re-write the 2 · x as a fraction by putting it
over a denominator of one. Doing this:
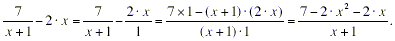
|