Adding and Substracting Fractions

In this section we look at the addition (and subtraction) of fractions. If fractions are to be added then they must have the same denominators .

Example

Write the following sums of fractions as single fractions.

Solution

a) Taking all the fractions with denominator 24,

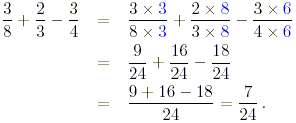
(b) This time, taking all the fractions with denominator 12,

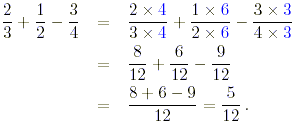
The exercise below is designed to give you some practice at addition and subtraction of fractions.

Exercise

Evaluate the following, putting the final answer in its lowest terms.

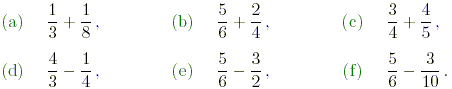
(a) The lowest common denominator is 24, so

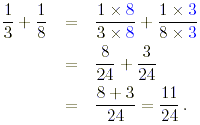
(b) Before proceeding, note that the second fraction is not in its lowest terms. Since 2/4=(1 × 2 )/(2 × 2 )=1/2,

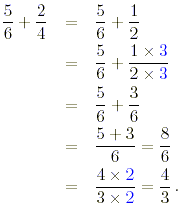
This fraction is called an improper fraction since the numerator is larger than the denominator. It is perfectly acceptable as a fraction but it may also written as .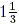

(c) The least common denominator of the two fractions is 20 so

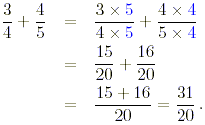
This is another improper fraction which may be written as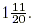

(d) The least common denominator of the two fractions is 12 so

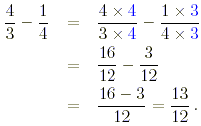
This is another improper fraction which is equal to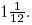

(e) The least common denominator of the two fractions is 6 so

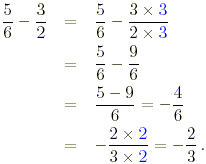
where the common factor 2 has been cancelled to obtain the final answer.

(f) The least common denominator of the two fractions is 30 so

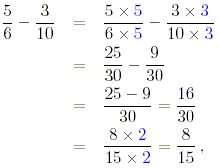
where the final answer is obtained after cancellation of the common factor 2.

To finish this section there follows two simple quizzes.

Quiz

Which of the following fractions is the result of evaluating the sum 3 4 - 2 3 + 1 6 ?

(a) 1/4, (b) 1/3, (c) 1/5, (d) 3/8.

Solution

The least common denominator of the three fractions is 12, so

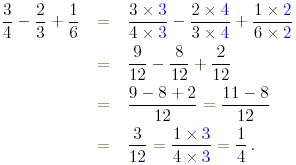
Quiz

From the fraction given below, choose the one which is mid-way between 2/3 and 4/5.

(a) 2/3, (b) 3/5, (c) 10/15 (d) 11/15.

Solution

The least common denominator of the two fractions is 15. Writing both fractions with this denominator gives

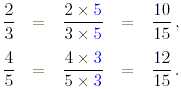
The fraction mid-way between 10/15 and 12/15 is 11/15.