Properties of Rational Exponents
The properties of integer exponents also hold for rational exponents. This
table contains an example of each property.
| Property |
Integer Exponents |
Rational Exponents |
| Multiplication |
32
· 34 = 32 + 4 = 36 |
37/5 · 33/5
= 37/5 + 3/5 = 310/5 = 32 = 9 |
| Division |
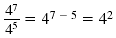 |
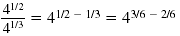 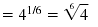 |
| Power of
a Power |
(52)3 = 52
· 3 = 56 |
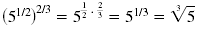 |
| Power of
a Product |
(5 · 7)3
= 53
· 73 |
(5 · 7)1/6 = 51/6
· 71/6
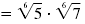 |
| Power of
a Quotient |
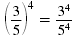 |
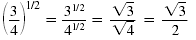 |
The Power of a Power Property is particularly useful when we work with
rational exponents.
| For example, let’s use this property to rewrite
53/4 in two different, but equivalent, ways.
|
Notation 1 53/4 |
Notation 2 53/4 |
| Rewrite the fraction 3/4 as 3
· (1/4) and as (1/4) · 3. |
= 53 · (1/4) |
= 5(1/4) · 3 |
| Use the Power of a Power Property. |
= (53)1/4 |
= (51/4)3 |
| Use radical notation. |
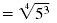 |
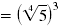 |
Thus,
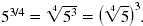
Let’s compare the original exponential expression, 53/4, with the final
radical expressions,
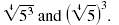 • In the original expression
53/4, the exponent is
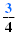 . .
• The denominator, 4, is the index of the radical
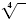 . .
• The numerator, 3, is a power in the radical expression.
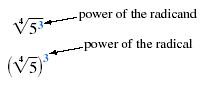
This relationship is true in general.
|