The FOIL Method
Consider how we find the product of two binomials x + 3 and x + 5 using the
distributive property twice:
| (x + 3)(x + 5) |
= (x + 3)x + (x + 3)5 |
Distributive property |
| |
= x2 + 3x + 5x + 15 |
Distributive property |
| |
= x2 + 8x + 15 |
Combine like terms. |
There are four terms in the product. The term x2 is the product of the first term of
each binomial. The term 5x is the product of the two outer terms, 5 and x. The term
3x is the product of the two inner terms, 3 and x. The term 15 is the product of the
last two terms in each binomial, 3 and 5. It may be helpful to connect the terms
multiplied by lines.
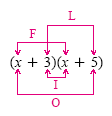 |
F = First terms O = Outer terms
I = Inner terms
L = Last terms |
So instead of writing out all of the steps in using the distributive property, we can
get the result by finding the products of the first, outer, inner, and last terms. This
method is called the FOIL method.
For example, let’s apply FOIL to the product (x - 3)(x + 4):
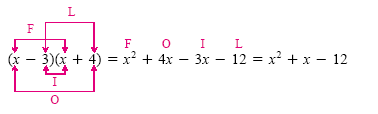
If the outer and inner products are like terms, you can save a step by writing down
only their sum.
Helpful Hint
The product of two binomials
always has four terms before
combining like terms. The
product of two trinomials
always has nine terms before
combining like terms. How
many terms are there in the
product of a binomial and
trinomial?
Example 1
Multiplying binomials
Use FOIL to find the products of the binomials.
a) (2x - 3)(3x + 4)
b) (2x3 + 5)(2x3 - 5)
c) (m + w)(2m - w)
d) (a + b)(a - 3)
Solution
a) (2x - 3)(3x + 4)
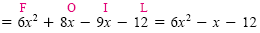
b) (2x3 + 5)(2x3 - 5)
= 4x6 - 10x3 + 10x3 - 25 = 4x6 - 25
c) (m + w)(2m - w) = 2m2 - mw +2mw - w2 = 2m2
+ mw - w2
d) (a + b)(a - 3) = a2 - 3a + ab - 3b There are no like terms.
|