Graphing Compound Inequalities

We can write compound inequalities with two variables just as we do for one variable. For example,

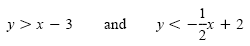
is a compound inequality. Because the inequalities are connected by the word and, a point is in the solution set to the compound inequality if and only if it is in the solution sets to both of the individual inequalities. So the graph of this compound inequality is the intersection of the solution sets to the individual inequalities.

Example 1

Graphing a compound inequality with and

Graph the compound inequality

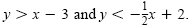
Solution

We first graph the equations y = x - 3 and 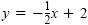. These lines divide the plane into four regions as shown in figure (a) below.

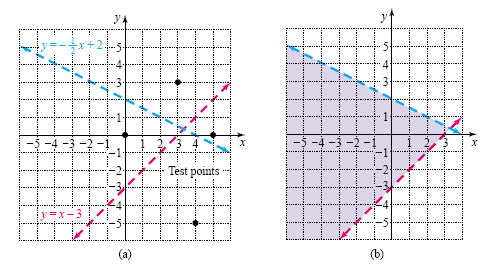
Now test one point of each region to determine which region satisfies the compound inequality. Test the points (3, 3), (0, 0), (4, -5), and (5, 0):

3	> 3 - 3	and	3		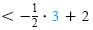Second inequality is incorrect.
0	> 0 - 3		0		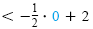Both inequalities are correct.
-5	> 4 - 3		-5		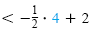First inequality is incorrect.
0	> 5 - 3		5		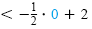Both inequalities are incorrect.

The only point that satisfies both inequalities is (0, 0). So the solution set to the compound inequality consists of all points in the region containing (0, 0). The graph of the compound inequality is shown in figure (b) above.

Compound inequalities are also formed by connecting individual inequalities with the word or. A point satisfies a compound inequality connected by or if and only if it satisfies one or the other or both of the individual inequalities. The graph is the union of the graphs of the individual inequalities.

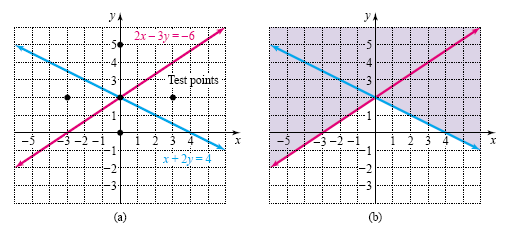
Example 2

Graphing a compound inequality with or

Graph the compound inequality 2x - 3y ≤ 6 or x + 2y ≥ 4.

Solution

First graph the lines 2x - 3y = -6 and x + 2y = 4. If we graph the lines using x- and y-intercepts, then we do not have to solve the equations for y. The lines are shown in figure (a) below. The graph of the compound inequality is the set of all points that satisfy either one inequality or the other (or both). Test the points (0, 0), (3, 2), (0, 5), and (-3, 2). You should verify that only (0, 0) fails to satisfy at least one of the inequalities. So only the region containing the origin is left unshaded. The graph of the compound inequality is shown in figure (b) below.

Helpful Hint

When graphing a compound inequality connected with“or,” shade the region that satisfies the first inequality and then shade the region that satisfies the second inequality. If the inequalities are connected with “and,” then you must be careful not to shade too much.