Complex Numbers
Imaginary numbers
The use of real positive numbers to describe the magnitude of actual quantities in the world (e.g. money) gives them an immediate significance.
This is a bit more difficult for negative numbers, though the concept of debt, say, makes their meaning clear.
Now we are going to consider a new type of number – imaginary numbers.
Let’s start by considering the solution of an arbitrary quadratic equation:
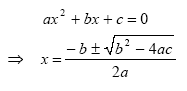
You have probably seen the case when the discriminant b2 - 4ac is
positive:
| |
x2 - 5x + 6 |
= 0 |
| → |
(x - 2)(x - 3) |
= 0 |
| → |
x = 3 |
or |
x |
= 2 |
But what happens if the discriminant b2 - 4ac is negative?
If the discriminant b2 - 4ac is negative, we have to take the square root of a negative number to solve the equation:
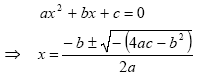
To do this, we use “imaginary numbers†by introducing some new notation:
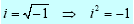
So the solution of the quadratic equation is written in terms of the imaginary number
i:
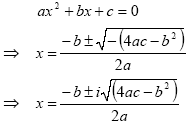
An imaginary number has the form iy where y is a real number and i2 = -1.
Examples of imaginary numbers:
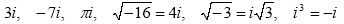
Addition and subtraction:
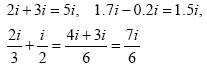
Multiplication:
the usual rules apply, but we use i2 = -1, too:
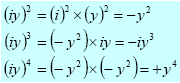
We use i2 = -1 to multiply two different imaginary numbers, so that for a and
b real:
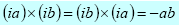
and for multiplication of a real and an imaginary number, we get an imaginary number:
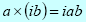
Division:
Division of an imaginary number by a real number:
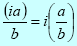
Division of an imaginary number by another imaginary number:
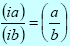
Division of a real number by an imaginary number:
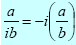
Useful identitiy:
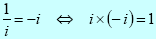
|