Factoring a Polynomial by Finding the GCF
Example 1Factor: 9wxy3 - 21w2y4 + 12w3xy2
Solution
| Step 1 Identify the terms of the polynomial. |
9wxy3, - 21w2y4, 12w3xy2
|
| Step 2 Factor each term. |
9wxy3 - 21w2y4
12w3xy2 |
= 3 · 3 · w · x
· y · y · y = -1 ·
3 · 7 · w · w · y · y · y · y
= 2 · 2 · 3 · w · w · w · x
· y · y |
| Step 3 Find the GCF of the terms.
In the lists, the common factors are 3, w, y, and y.
The GCF is 3 · w
· y · y = 3wy2. |
|
| Step 4 Rewrite each term using the GCF. To help keep the signs
straight, write the
subtraction of 21w2y4
as addition of -21w2y4. Rewrite each term
using 3wy2 as a factor. |
=
= |
9wxy3 - 21w2y4 + 12w3xy2
9wxy3 + (-21w2y4) + 12w3xy2
3wy2 · 3xy + 3wy2
· (-7wy2) + 3wy2
· 4w2x |
| Step 5 Factor out the GCF. Factor 3wy2. |
= |
3wy2(3xy -7wy2
+ 4w2x) |
Thus, 9wxy3 - 21w2y4 + 12w3xy2
= 3wy2(3xy -7wy2
+ 4w2x)
You can multiply to check the factorization. We leave the check to you.
Note:
Another way to decide which terms belong
inside the parentheses is to ask:
“3wy2 times what gives 9wxy3?â€
Answer: 3xy
“3wy2 times what gives -21w2y4?â€
Answer: -7wy2
“3wy2 times what gives 12w3xy2?â€
Answer: 4w2x
Example 2
Rewrite 5 - x as a product by factoring out -1.
Solution
| Identify the terms of the polynomial. |
5 and -x |
| Rewrite each term using -1 as a factor. |
5
-x |
= -1 · -5
= -1 · x |
| We can write: |
|
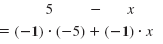 |
| Factor out -1- |
|
= -1(-5 + x) |
| We usually write terms with variables first.
So, we use the Commutative Property of
Addition to rearrange the terms inside
the parentheses. So we can write 5 - x as -1(x - 5). We multiply to check the factorization. |
|
= -1(x - 5) |
| Is Is
Is |
-1(x - 5)
-1 · x + (-1) · (-5)
- x + 5 |
= 5 - x ? = 5 - x ?
= 5 - x ? Yes |
|