Solving Quadratic Equations

Solving quadratic equations means to find when the branches crosses the x axis. Completing the square finds the max/min point (vertex) which can be helpful for some  types of questions, but other types of question ask about points that cross the axis.

In order to solve the problem:

1. there are several ways to start this process. In grade ten you learned two:

a. Factoring

i. Using simple or complex factoring techniques find the points and

solve for 0 = (x + a)(x + b)

b. Quadratic Equation

i. The plug and play solving method

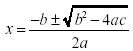
c. The new method is to us completing the square to solve the equation for the roots

i. Complete the square so that it is in the form 0 = a (x + h) ² + k

ii. arrange the equation so that the square is on one side and the constant is on the other.

iii. Solve for the variable using exponent laws (since it is always squared, both sides are square rooted)

iv. Isolate for the variable

Possible outcomes for roots of a Quadratic equation:

1. 2 real roots

a. notice the values of the coeffiecients

i. if the vertex is above the x axis AND a is negative, then 2 real

roots.

ii. If the vertex is below the x axis and the value of a is positive, then

there are two real roots

2. 1 real root

a. notice there is no vertical displacement. If the vertex is on the x axis there is only 1 real root

3. no real roots (therefore two complex roots)

a. notice the location of the vertex

i. the vertex is above the x axis and the parabola points up, there are no real roots (the graph never crosses the x axis)

ii. the vertex is below the x axis and the parabola points down, there are no real roots. (the graph never crosses the x axis)

Example 1

kx - 8 = 2x ²

What values does k have for two distinct real roots, one real root or no real roots.

Two real roots

-2x ²  + kx - 8 > 0

k ² - 4(-2)(-8) > 0

k ² > 64

k > 8; k < -8

one root

no roots