Power of a Product and Power of a Quotient
Power of a Product
Consider an example of raising a monomial to a power. We will use known rules
to rewrite the expression.
| (2x)3 |
= 2x · 2x · 2x |
Definition of exponent 3 |
| |
= 2 · 2 · 2 · x · x · x |
Commutative and associative properties |
| |
= 23x3 |
Definition of exponents |
Note that the power 3 is applied to each factor of the product. This example
illustrates the power of a product rule.
Power of a Product Rule
If a and b are real numbers and n is a positive integer, then (ab)n
= an bn.
Example 1
Using the power of a product rule
Simplify. Assume that the variables are nonzero.
a) (xy3)5
b) (-3m)3
c) (2x3y2z7)3
Solution
| a) (xy3)5 |
= x5(y3)5 |
Power of a product rule |
| |
= x5y15 |
Power rule |
| b) (-3m)3 |
= (-3)3m3 |
Power of a product rule |
| |
= 27m3 |
(-3)(-3)(-3) = -27 |
c) (2x3y2z7)3 = 23(x)3(y2)3(z7)3
= 8x9y6z21
Power of a Quotient
Raising a quotient to a power is similar to raising a product to a power:
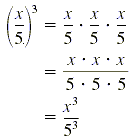 |
Definition of exponent 3 Definition of multiplication of
fractions
Definition of exponents |
The power is applied to both the numerator and denominator. This example
illustrates the power of a quotient rule.
Power of a Quotient Rule
If a and b are real numbers, b ≠ 0, and n is a
positive integer, then
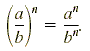
Example 2
Using the power of a quotient rule
Simplify. Assume that the variables are nonzero.
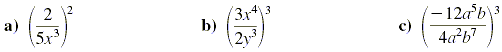
Solution
a)
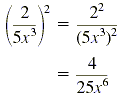 |
Power of a quotient rule
(5x3)2 = 5x(x3)2 = 25x6 |
b)
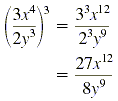 |
Power of a quotient and power of a product rules
Simplify |
c) Use the quotient rule to simplify the expression inside the parentheses
before using the power of a quotient rule.
|