Simplifying Cube Roots That Contain Integers

To simplify a cube-root radical, we look for perfect cube factors of the radicand.

Example 1

Simplify:

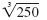
Solution
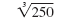Write the prime factorization of 250.
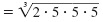Group triples of like factors to form perfect cubes.
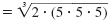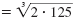Write as a product of two radicals.
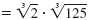Simplify

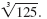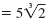Thus, in simplified form,

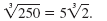
Note:

If you realize that 125 is the largest perfect cube factor of 250, then you can write:

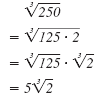
Example 2

Simplify:

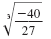
Solution

To simplify this expression, we’ll use the Division Property of Cube Roots to rewrite the radical as a quotient of radicals. Then we’ll simplify each of those radicals.
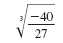Write the numerator and denominator under separate radical symbols.
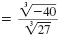Write -40 using a perfect cube factor, -8.
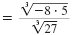Write the numerator as the product of two radicals.
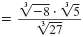Simplify the cube roots of any perfect cubes.

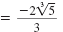Thus, in simplified form,

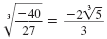
Note:

If you have difficulty seeing the largest perfect cube that is a factor of -40 or 27, write their prime factorizations.
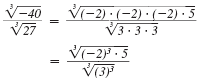