Solving Absolute Value Inequalities
Solving an Absolute Value Inequality of the
Form | x| > a
Example 1
Solve: -10 + 4|2x - 7| > 50
| Solution
Step 1 Isolate the absolute value.
Add 10 to both sides.
Divide both sides by 4.
Step 2 Make the substitution w = 2x - 7.
Step 3 Use the Absolute Value
Principle to solve for w. Step 4 Replace w with 2x - 7.
Step 5 Solve for x.
Add 7 to both sides.
Divide both sides by 2.
Step 6 Check the answer.
We leave the check to you.
So, the solution is x < -4 or x
> 11. |
-10 + 4|2x - 7| > 50
4|2x - 7| > 60
|2x - 7| > 15
|w| > 15
w < -15 or w > 15
2x - 7 < -15 or 2x - 7 > 15
2x < -8 or 2x > 22
x < -4 or x > 11 |
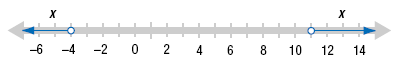
Example 2
Solve: -5|x| - 12 < 28
| Solution Step 1 Isolate the absolute value.
Add 12 to both sides.
Divide both sides by -5 and reverse the
direction of the inequality symbol. |
-5|x| - 12 < 28
-5|x| < 40
|x| > -8 |
Since |x| represents a nonnegative number, it is greater than
-8 for all
values of x.
Therefore, the solution is all real numbers.
|